Distinguiendo el Análisis Factorial Confirmatorio de la Regresión Simple en Modelos de Ecuaciones Estructurales

Modelo de Análisis Factorial Confirmatorio (CFA):

• Se utiliza para validar la estructura de los factores propuesta teóricamente.
• Cada factor latente está definido por un conjunto de variables observadas que se supone que son manifestaciones del mismo constructo subyacente.
• No hay flechas directas de un factor a otro, sino una correlación entre ellos, lo que sugiere que los factores pueden estar relacionados, pero no necesariamente en una relación causal.
• Los términos de error (E7* a E17*) están asociados con cada variable observada y representan la varianza no explicada por el factor latente.
• Factores Latentes: F1* y F2*, representados por círculos, son los constructos teóricos no observados que el análisis está tratando de medir. Se asume que estos factores subyacen a las respuestas o mediciones observadas.
• }Variables Observadas: Indicadas por los cuadros amarillos, V7 a V11 se asocian con F1*, y V12 a V17 se asocian con F2*. Estas son las respuestas medidas o ítems que se utilizan para representar los factores latentes.
• Cargas Factoriales: Los números 1.0 junto a las flechas indican las cargas factoriales estandarizadas de las variables observadas en los factores correspondientes, sugiriendo que estas relaciones son fijas o se han estandarizado para identificar la escala de los factores.
• Errores de las Variables Observadas (E7-E17)**: Estos términos, representados por pequeños cuadros al final de cada variable observada, reflejan la variación o el error en las mediciones que no es capturado por los factores latentes.
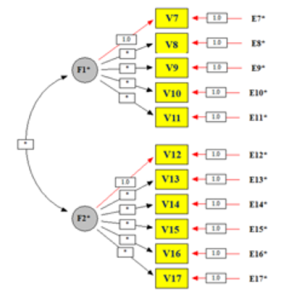
• Correlación/Covarianza entre Factores Latentes: La flecha curva de doble punta entre F1* y F2* indica que existe una relación estadística entre los dos factores latentes, que podría ser una correlación o covarianza, permitiendo que los factores co-varíen o se relacionen entre sí en el modelo. La Figura 1 muestra un analisis factorial confirmatorio

Figura 1

Analisis factorial confirmatorio

Modelo de Regresión Simple:

• Incluye una variable independiente, el término de perturbación D1*, que tiene una influencia causal directa sobre el factor latente F1.
• Existe una flecha directa de F1 a F2, indicando una relación causal donde F1 influye directamente en F2.
• Este modelo va más allá de la validación estructural del CFA al examinar cómo un factor puede influir causalmente en otro.
• Al igual que en el CFA, hay términos de error para cada variable observada (E7* a E17*).

• D1*: Representa un término de perturbación para el factor F1, sugiriendo que D1* captura la variabilidad o los efectos causales en F1 que no son explicados por el modelo.

• Factores Latentes (F1 y F2): Estos círculos simbolizan los constructos teóricos que se están midiendo indirectamente a través de las variables observadas (V7-V17). La flecha que apunta de F1 a F2 indica una relación causal propuesta, donde F1 tiene un efecto directo sobre F2.
• Variables Observadas: Las cajas amarillas (V7-V17) son las variables medibles que sirven como indicadores de los constructos latentes F1 y F2.
• Cargas Factoriales: El número 1.0 al lado de las flechas que conectan los factores latentes con sus variables observadas implica que la carga factorial está estandarizada o fijada, probablemente para la identificación del modelo.
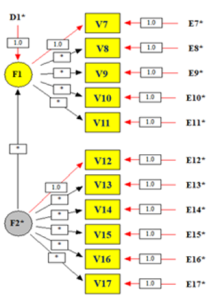
• Errores de las Variables Observadas (E7-E17)**: Representan la variabilidad de cada variable observada que no es explicada por el factor latente correspondiente. La Figura 2 muestra un ejemplo del modelo de regresión.

Figura 2

Modelo de regresión siempre